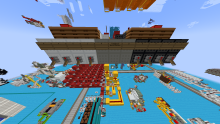
It calculates A modulo B for four-bit inputs A and B, using redstone signal strength.
The white input is A, the black input is B.
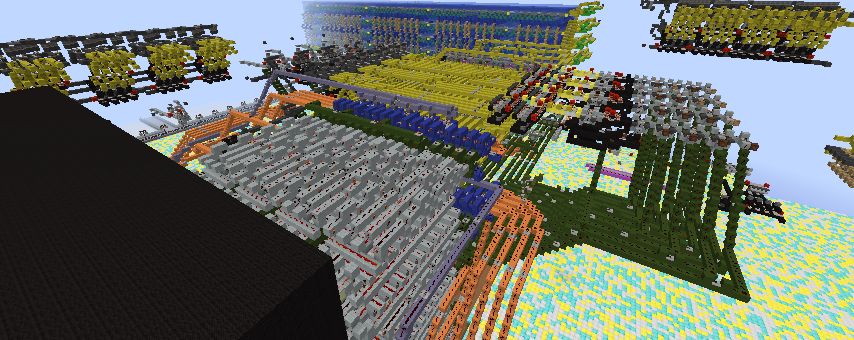
The white and black circuits convert the binary inputs into signal strength.
The red circuit then repeatedly subtracts B from A until it gets to zero. If the subtraction left a result more than 0, the result is passed down one of the staircases. The last staircase (in lime) is reserved for the special case of dividing by zero, and blocks the signal from being passed at all, thus outputting zero.
The orange circuit makes every powered red line block the signal of the one before it, so only the last powered line ends up transmitting the signal. This is guaranteed to have a signal strength between 1 and B inclusive.
However, the modulo function's output ranges from 0 to B-1. The difference lies in the behavior when A is an exact multiple of B, where this outputs B but the modulo function outputs 0.
To fix this, the yellow circuit checks that the output is less than B by subtracting B-1. If the result is 1, then the signal is blocked to output 0 rather than B. If the output is less than B (i.e. less than or equal to B-1) it proceeds to the lamp display. The number of lamps powered is equal to A modulo B
Flip the levers to set A and B, wait a few seconds, then check the lamp display at the bottom.



Comments
Denied
You build a nice functional modulo machine.
If built like this, if is a "fairly simple" machine - if you boil it down to what it does.
But making it small and fast counts. Currently it uses a huge contraption to cancel out the previous line. That can be made much smaller (as I showed in game). Doing so would massively improve the quality of this build.
This build alone will sadly not give you the Tinkerer rank if built super nicely, due to its low complexity.
But keep up the good work and build some more machines of this grade and the promotion will be in near future :)