

-= Computational Features =-
Architecture: SUBLEQ (Harvard implementation)
Data width: 4 Bits
Instruction width: 12 Bits (6-bit Branch address + 3 * 2-bit operands)
Memories:
- Up to 64 words of Instruction ROM (16 installed)
- 4 Registers
- 4 Register ROM words (Used to initialise the registers on reset)
- Register 3's writes are mapped to a 7-segment display
-= Hardware Features =-
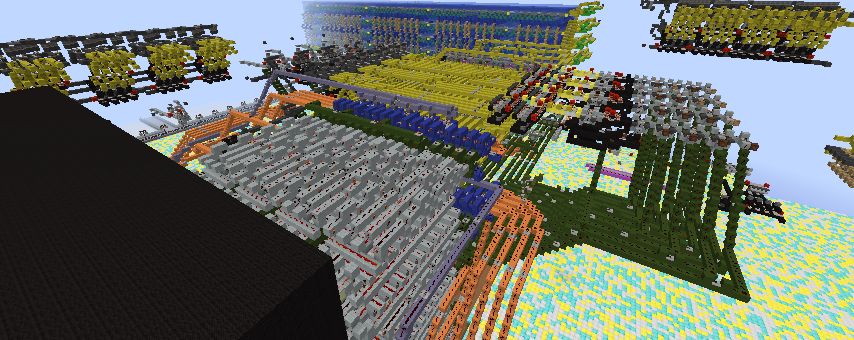
- Torch programmable ROMs
- ALU (Subtractor), Registers and Program counter designed by me
- CLE based subtractor
- True dual read registers
- 32 tick clock speed (64 gt)
- Run mode or single cycle step
- Reset with 1 button
- Flat top 7-segment dust display designed by LAM678 and myself
- 6 blocks in height
- 16 instruction words built but can be expanded to 64
This is a simple 4-bit computer which uses the SUBLEQ architecture.
It only has 1 instruction: SUBLEQ, which is short for:
Subtract and Branch if Less than or Equal to Zero
Despite only having this 1 instruction, SUBLEQ CPUs are Turing-complete and can run theoretically run fully fledged programs. The architecture works on 4 operands: Source-A, Source-B, Destination, Branch Address. Labelling these as A, B, C and D respectively:
The contents of memory address B are subtracted from the contents of memory address A. The result is written back to memory address C, and if the result produced is less than or equal to zero, the program control will be transferred to address D. If not, the program control will continue to the next instruction.
The computer uses a Harvard implementation where the data and instruction memories are separated.
The program counter is 6 bits, so it can support 64 instruction words, each being 12 bit. Only 16 instructions are fitted currently, but more can be added with the cost of +2 ticks per cycle per 8 instructions.
The subtractor circuit in the computer is CLE-based. I made a 3t horizontal CLE not long ago, and I converted it to become a 4t subtractor which is the arithmetic basis of the computer. I also made horizontal true dual-read registers which read onto an interlaced bus of 8 bits, splitting out into the subtractor's inputs. The program counter is 6-bit and it is also my design, it is parallel too because it uses instant diodes like CLEs do. The counter works as a lower 4 bits and then an upper 2 bits with a 1 tick extension because of signal strength.
The computer's name is Lorna.
There are two ROMs - one that initialises the registers with constant values, and one that holds the program.
The program ROM is 12-bit, the upper 6 bits correspond to a branch address. The next 2 bits are Source A, the next 2 are Source B and the final 2 are the Destination register.
In these ROMs you will find a Fibonacci program coded in. To the right hand side of the instruction ROM there's a set of CPU controls. To start the Fibonacci you need to press Reset, then flick the Run lever to start the program. The Fibonacci numbers will appear on the 7-segment hex display on the other side of the processor. To perform addition, one has to flip the sign of a number first and then subtract with it as B. This is what allows Fibonacci to be possible. I've also tested a 0 to 9 counting program for this computer.
The 7-segment display is made by LAM678 and myself. It uses a red-coder and a lookup-table to interpret signal strength input to any hexadecimal digit. I connected it to the computer, where all writes to Register 3 are mirrored to the display. The Fibonacci program copies each new number to register 3, thus displaying them.
Sadly the capabilities of the computer are limited due to memory. Perhaps an 8 or 16 register design with RAM support could perform even more complex tasks, even simple games.

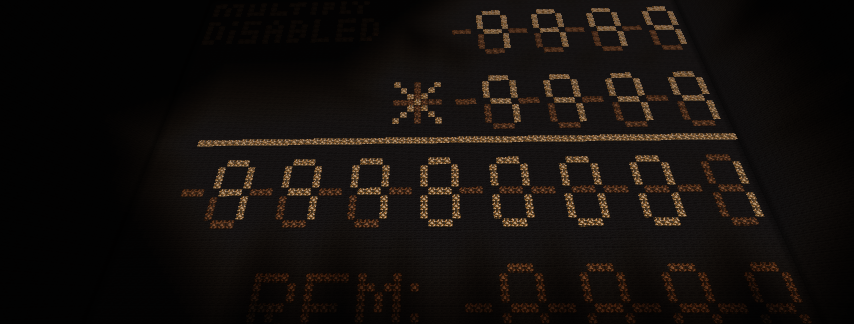


Comments
About the branch
I was told that a showcase of conditional logic is required to pass for Regular, and my Fibonacci program was unconditionally looping. So:
I modified the program to stop once it encountered an arithmetic overflow! Since the condition works on 2's complement (negative or zero), the highest number it can reach in 4 bits for the Fib. sequence is 5. It works!