I know how to create an adder, and I know how to make that adder subtract, as long as you understand how negative numbers work in binary code. But I still don't think it can qualify as an ALU, all it can do is addition and subtraction. Multiplication and division are going to be harder, but multiplication seemed easier, so I started with that.
Before I created any circuits, I first needed to figure out what kind of algorithm I needed to make in order to successfully multiply one number by the other. Here's what I derived:
You input two numbers, number A, and number B, which go into inputs A and inputs B, allocated to the two different total numbers you input into the machine, rather than individual inputs. Number B branches off into a secondary area, where it enters into a circuit that has the ability to pulse a signal the exact number of times that the inputted number dictates. Each time this signal pulses, it will add number A to itself.
I then had to figure out the specifics:
In order to add number A to itself, I needed to input number A into inputs B. So, when you initially input numbers A and B, instead of number B secondarily branching off into the pulsing circuit, it will branch off primarily to the pulsing circuit, leaving inputs B completely empty, but the value still stored in the pulsing section. From there, the output of the ALU will automatically be whatever number A is, as it has added nothing to number A, because inputs B are now completely empty. This means that feeding the output into inputs B mimics the behavior of copying number A into inputs B. We connect the output to inputs B, but attach a locked repeater to each one of the output wires going into inputs B, and the repeaters will only be unlocked if the pulse circuit pulses. So, while the circuit has not pulsed yet, the output cannot make its way to inputs B. However, when the circuit does pulse, it is able to reach inputs B. Normally, this would cause a constant feedback loop of adding the numbers together continuously until it reaches the integer limit. However, because we are only unlocking these repeaters for a moment, because they are merely being pulsed, the ALU doesn't have enough time to calculate the answer, output that, and put that back into the repeaters, before they become locked again. No exceptions.
Example:
5 x 3 -
Number A = 5, and number B = 3. Number B goes into the pulse section of the ALU, and then gets removed from inputs B, leaving inputs B blank. This leaves only inputs A on, with number A, 5, being displayed. This means that the ALU is only going to output 5, or 101. But right now, that output can't make its way to inputs B, as the repeaters are currently locked. Then, when you flick the lever, the process begins. The circuit reads the number 3, or 11, and so pulses three times. Each time it pulses, it momentarily unlocks the repeaters, which will update its value to whatever the output is. This will allow the output signal to be fed back into inputs B. But then, the repeaters are locked again, because it was only a momentary pulse, so by the time the circuit adds the two numbers together, the repeaters are locked again. In this case, the value it looped back in was 101, or 5, so now the equation inputted is 101 + 101 (technically 00000101 + 00000101), which is 1010, or ten. So, the new output of the ALU is now 1010. Then, the circuit pulses a second time, and updates the repeaters. So now, the value 1010 is fed into inputs B, which will change the equation to 101 + 1010, which is 1111, or 15. The circuit then pulses one final time, and updates the repeaters, so now the value 1111 is being fed into inputs B, which will change the equation to 101 + 1111, which is 10100, or 20. The circuit has pulsed for the final time, so the operation has now been completed. We did 101 x 11, or 5 x 3, and got 10100, or 20. This is incorrect, as 5 x 3 = 15, not 20. The reason this is one iteration more is because the circuit pulses the number of times the number says, which means if you inputted the number 1, it would pulse one time, adding number A to itself one time. This does not mimic the behavior of multiplying number A by 1, as 1x = x, so we need to find a way to reduce it. We could simply run the number through a circuit that reduces the value of the number by 1 perhaps.
So, now that we have completed an operation, we need a way to reset it. Currently, the value 1111 is being stored in inputs B, which was useful when we needed it, but now we don't, so we need to get rid of it. To do this, we simply press a button that will forcefully shut off all of the outputs momentarily, unlock all the repeaters, lock them again, and then shut off the mechanism that turns off all the outputs, leaving the outputs to be whatever they were before hand. Also, this button will erase whatever is stored within the pulsing circuit, as we do not need that value anymore.
This is the algorithm for how to multiply two numbers together using a binary code adder. I do have some ideas on how to actually make the circuitry, and I am currently working on the pulsing circuit, as that is the most complicated part of this whole operation. I'll make an update on that once I have the pulsing circuit completed, it is decently difficult to figure out.

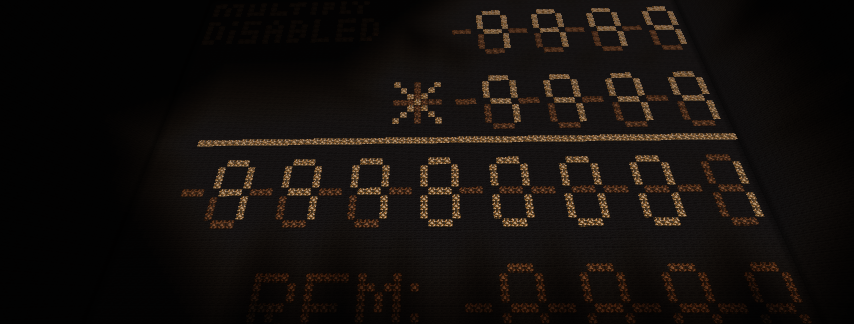


Bruh how did I just realize that 5 x 3 = 15
Eh, that just means I'll have to pulse the machine one less times.